

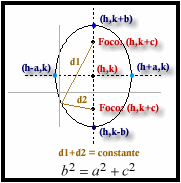
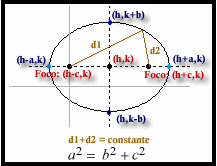
Se llama elipse al lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos, llamados focos, es una constante.
La línea que une los dos focos se llama eje principal de la elipse y la mediatriz de los mismos eje secundario.
Se llaman vértices de la elipse a los puntos donde ésta corta a sus ejes.
El punto medio de los dos focos se llama centro de la elipse y la distancia entre ellos se llama distancia focal.
![]()
Generalmente el eje principal se representa por
2a y la distancia focal por 2c. Los valores a y c se
llaman semieje principal y semidistancia focal, respectivamente.
Cálculo del eje secundario
Llamando 2b al eje secundario, P al vértice superior, O al centro y F y F ' a los focos de la elipse, por el teorema de Pitágoras:
![]()
![]()
![]()
Por definición de elipse
![]()
![]()
A la distancia b se le llama semieje secundario.
Radio vector
Las distancias desde un punto de la elipse hasta cada uno de los focos se llaman radios vectores correspondientes a dicho punto.
Para simplificar los cálculos, se supondrá inicialmente una elipse cuyo centro es el origen de coordenadas y cuyos focos se encuentran en el eje de abscisas. Así los focos serán F(c, 0) y F ''(-c, 0) y los ejes de la elipse son los ejes de coordenadas.
Cálculo de los radios vectores
Dado un punto P(x, y) de una elipse centrada en el origen y con focos en F(c, 0) y F'(-c, 0) se tiene:
![]()
![]()
Demostración:
Si el punto pertenece a la elipse, ha de ser:
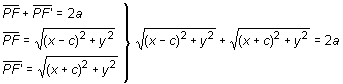
Operando:
![]()
![]()
![]()
![]()
![]()
![]()
Ecuación canónica de la elipse
La ecuación de una elipse centrada en el origen y con focos en F(c, 0) y F'' (-c, 0) es
![]()
Demostración:
Sustituyendo en la fórmula de uno cualquiera de los radios vectores se obtiene:
![]()
![]()
![]()
Þ a2x2 + a2c2 + a2y2 = a4 + c2x2 Þ
Þ a2x2 + a2c2 + a2y2 = a4 + c2x2 Þ
![]()
![]()
![]()
(0, b) y (0, -b).
Demostración:
Los vértices son los puntos donde la elipse corta a sus ejes. Se calculan por separado para cada eje:
· Eje principal:
El eje principal es el eje de abscisas, es decir y = 0. Para hallar su intersección con la elipse se resuelve el sistema:
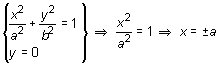
Los vértices son (a, 0) y (-a, 0)
· Eje secundario:
Se resuelve el sistema:
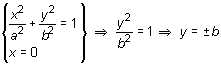
Los otros dos vértices son (0, b) y (0, -b)
Ecuación de una elipse con ejes paralelos a los ejes de coordenadas
Si una elipse tiene sus ejes paralelos a los ejes de coordenadas y su centro en el punto (x0, y0), los puntos de esta elipse se pueden trasladar mediante el vector -x01 - y02 y obtener una elipse centrada en el origen.
Entonces el punto que ha de verificar la ecuación canónica es (x - x0, y - y0). Por tanto, su ecuación es:
![]()
Desarrollando esta ecuación, se obtiene:
b2x2 - 2b2x0 x + b2x02 + a2y2 - 2a2 y0y + a2y02 - a2b2 = 0,
que se puede poner en la forma:
Ax2 + By2 + Cx + Dy + E = 0, donde A y B son del mismo signo.
Ecuación de una elipse vertical
Si una elipse tiene su eje principal vertical, su ecuación viene dada por:
![]()
Los vértices son los puntos (x0 ± b, y0) y (x0, y0 ± a) y los focos son (x0, y0 ± c).
Reducción de la ecuación de una elipse
![]()
Dada una ecuación del tipo Ax2 + By2 + Cx + Dy + E = 0, ésta puede transformarse
por el método que se verá en los ejercicios de aplicación. Dicha ecuación se llama ecuación
reducida de la elipse.
Si el segundo miembro fuese 1, se tendría una elipse centrada en (x0, y0). Los ejes
de la elipse son las rectas x = x0 e y = y0. Los vértices son (x0 ± a, y0) y (x0, y0 ± b).
En otro caso, como una suma de cuadrados es siempre positiva, se tendría que ningún punto la verifica y se habla de una elipse imaginaria.