

![]()
![]()
Se llama parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija llamada directriz.
La distancia entre el foco y la directriz de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p).
Dada una parábola, se llama eje de la misma la recta que contiene al foco y es perpendicular a la directriz.
Se llama vértice de la parábola al punto donde ésta corta a su eje.
Para simplificar la parábola, se supondrá que el vértice es el origen de coordenadas y que el foco se encuentra en el semieje positivo de abscisas.
Ecuación canónica de la parábola
La ecuación de la parábola con vértice en el origen de coordenadas y foco en el punto F(P/2,0) es y = 2px
Demostración:
![]()
![]()
La condición para que el punto esté en la parábola es que ambas coincidan
![]()
Elevando al cuadrado
-px + y2 = px Þ y2 = 2px
Hay otros tres casos elementales de parábolas:
· Si el eje es horizontal y el foco está en el semieje negativo de abscisas, la ecuación es y2 = -2px.
· Si el eje es vertical y el foco está en el semieje positivo de ordenadas, la ecuación es x2 = 2py.
· Si el eje es vertical y el foco está en el semieje negativo de ordenadas, la ecuación es x2 = -2py.
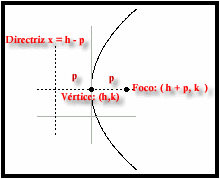
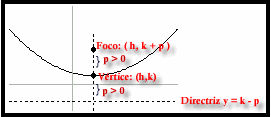
Parábola con vértice en un punto cualquiera
![]()
Si el vértice de una parábola se encuentra en
un punto (x0, y0) su ecuación será, según los casos:
· Eje horizontal y foco a la derecha: (y-y0)2 = 2p(x-x0)
· Eje horizontal y foco a la izquierda: (y-y0)2 = -2p(x-x0)
· Eje vertical y foco por encima: (x-x0)2 = 2p(y-y0)
· Eje vertical y foco por debajo: (x-x0)2 = -2p(y-y0)
Reducción de la ecuación de una parábola
Dada una ecuación del tipo Ax2 + Bx + Cy + D = 0 o del tipo Ay2 + Bx + Cy + D = 0, siempre es posible reducirla a la ecuación de una parábola. Para ello se completa un cuadrado y se manipula adecuadamente el otro miembro.
![]()
![]()